Quantum Science and Technology Hackathon
- Details
- Written by Andrea Sadlowski
- Category: Education
About the Quantum Science and Technology Hackthon - Design of the Hackathon
Among the many quantum related activities supported this year, IEEE is proud to have been a sponsor for the Quantum Science and Technology Hackathon (QSTH 2022). The Hackathon was designed as an attempt to stir the Quantum Ecosystem and enable people to think and implement new ideas/projects in Quantum. The aim was to create startups from scratch and also provide a platform for projects to move forward. The Hackathon started on the 15th of August 2022 and the final presentation and Winners selection happened on the 18th of November 2022.
The Hackathon was conducted in 3 phases:
- Ideation Phase
- Prototype Development Phase
- Final Shortlist Phase
The full timeline for all 3 phases, beginning with launch of the hackathon in August 2022, and ending with the wrap-up in November is shown below.

Global Reach and Participant Stastics
Organised by the Quantum Ecosystems Technology Counil of India, the Quantum Science and Technology Hackathon attracted interantional participants from diverse backgrounds. Some interesting statistics related to the Hackathon are captured in the illustrations below.
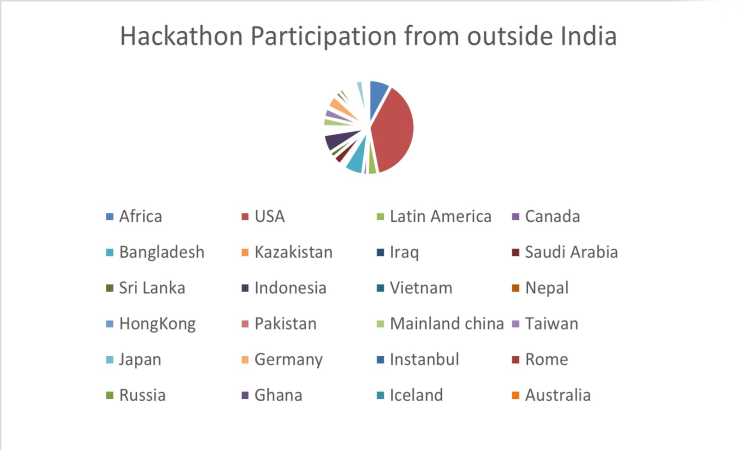
With 1626 individual registrants, the QSTH hackathon 2022 participants made up a large community. The attached pic shows the distribution of people who registered from outside India, representing 24 additional countries. This distribution is especially interesting, since QSTH did not do much of an International Outreach for the Hackathon. As a value we are focussed on International Collaboration in Science and Technology and hence this picture shows us that it is possible to create a stronger collaboration base in Quantum from India.
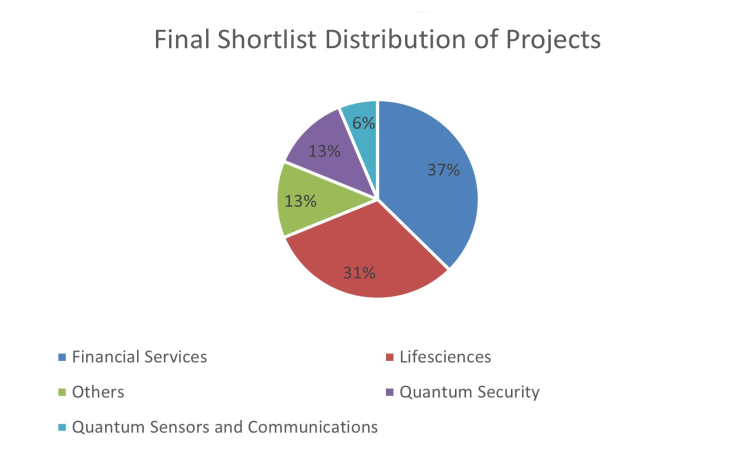
The various categories under which people could submit projects were Financial Service, Lifesciences, Quantum Security, Quantum Sensors and Communications and Others. As you can see in the charts there was a fair distribution of the various categories in the final shortlist. Although as you look at the Winners below , there is many more from the Lifesciences category .
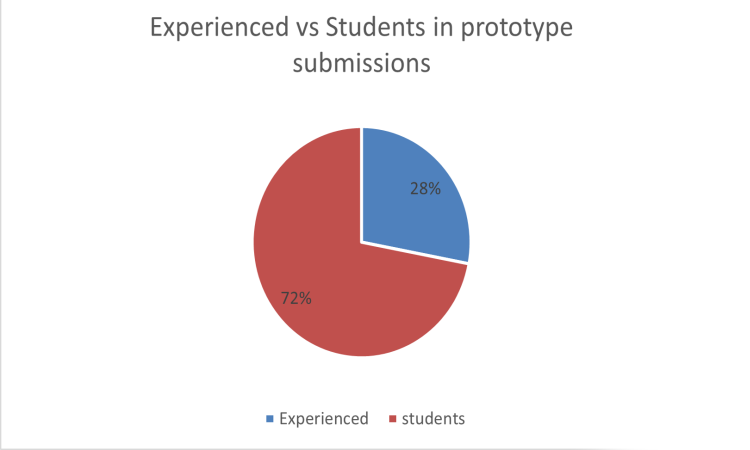
There was a fair amount of participation from experienced professionals, although students dominated the participation, with 72% of submissions coming from students, compared to 28% coming from professionals.
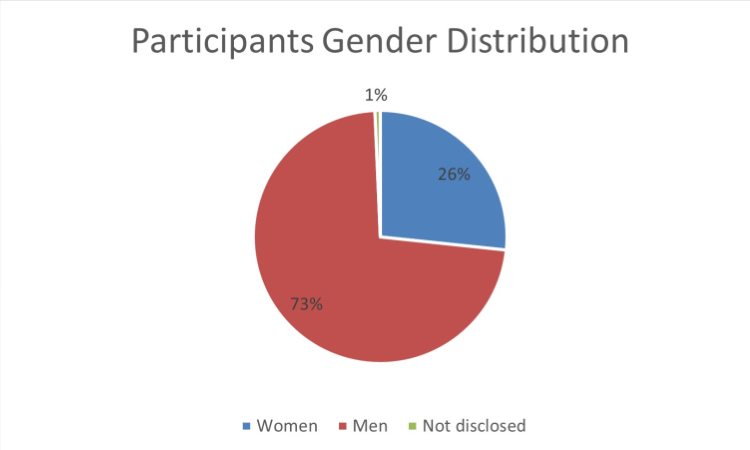
The participartion from women was 27% and we had 2 women lead teams in the announced prizes.
Congratulations to the 2022 WSTH Winners!
FIRST PRIZE - Team Name: SybilSys
Project: Qule - Exploring Chemical Infinities
Category: LifeSciences
Congratulations to Sabarikirishwaran Ponnambalam @Tarush Singh Sphoorthy Nadimpalli @Shubhang Mathur @Padmapriya Mohan
SECOND PRIZE: DeQuani from Defence Research and Development Laboratory (DRDL) - DRDO
Project:Design and Implementation of a Quantum safe cryptography algorithm using Polynomials to mitigate key-size based attacks
Category:Quantum Security
Congratulations! Ramkumar Ketti Ramachandran, Bhupendra Singh, Dr. Amanpreet Kaur, Taniya Hasija, Vaneeta Bhardwaj
THIRD PRIZE: AXIS. An all women team . One person from USA and one from Russia
Project:Compute the mean electric axis of the heart on IBM quantum hardware. Make the heart axis prediction using the DWave Quantum Annealers.
Category:Lifesciences
Congratulations! @Elena Suraeva @Olga Ok
SPECIAL MENTION1: Quantum Makers
Team from Tech Mahindra
Project : Using QGANs with adaptive training data for small molecule drug discovery
Category:Lifesciences
Congratulations Saket Apte Vinay Sharma Nikunj Sujit Odayoth @Vedant Gupta
SPECIAL MENTION 2: Q3DPredictor
Team from Qkrishi ( Indian Quantum Startup)
Project: Efficient Prediction of 3D Structure of Proteins using Quantum Algorithms
Category: Lifesciences
Congratulations! @Deshpande Sangram , V Raghavendra Harishankar P V Anant Sharma Janani A
Acknowledgements
The Hackathon took the support of Volunteers, mentors and Judges from around the globe. Literally the global Quantum Village came together to make this Hackathon happen. Thank you to our Volunteers , Mentors and Judges . The participants voted from the Best Mentor Award and Aneel Mitra and Divya Perumal were voted as the best mentors ! Congratulations!
Summary of the IEEE Workshop on Benchmarking Quantum Computational Devices and Systems
- Details
- Written by Chris Franzino
- Category: Education
This page is based on presentations at ICRC 2019 in San Mateo, CA. The views expressed by the speakers are theirs alone.
How is quantum computer performance assessed?
Benchmarks for conventional computers are standardized methods that test and evaluate hardware, software, and systems for computing. The results from these tests are expressed using metrics that measure features and behaviors of the system such as speed and accuracy. With the advent of quantum computers, new benchmarks are needed to address these same metrics while also accounting for differences in the underlying technologies and computational models.
While conventional computers rarely fail to operate as designed, current quantum computing systems are susceptible to large error rates. This dramatic difference in technological readiness influences the design and purpose of the quantum computing benchmarks, which are currently focused on identifying the scaling behavior with respect to size and error rates. This may include measuring coherence times or scattering rates specific to quantum technologies alongside the speed and accuracy familiar from conventional computers.
For example, ion trap technology for quantum computing, the stability of the trap frequency, the duration of a gate operation, and the stability of the control lasers all represent unique measures of performance. Similarly, for superconducting technologies, the precision of the Josephson, anhamonicity, and gate duration, are equally relevant to performance. The operation of these devices emphasize additional concerns in the controllability and scalability of the device and system, which can be addressed through more holistic benchmark methods based on gate error rates and circuit fidelities.
Benchmarks and metrics must also account for the differences between the underlying computing model. Currently, the gate- and adiabatic/annealing models of quantum computing represent different approaches to designing and operating quantum computing devices, and the benchmarks are tailored to these architectures in order to account for those differences. These differences also give rise to a different in size of the available quantum computers -- gate-models support less than 100 qubits currently while quantum annealers support up to 2,048 qubits. These differences in system capacity underscore the need for a diversity of approach to metrics and benchmarks for quantum computing.
See introductory video, Travis Humble, Kevin Young, Cathy McGeoch. 2:13 to 17:13
What is quantum supremacy and cross-entropy benchmarking?
The material on this section cross-entropy benchmarking and quantum supremacy was recently published in Nature by authors from Google.1
To benchmark quantum computers, you run quantum circuits from a set of single- and two-qubit gates and measure the resulting data string outputs of zeros and ones. Some data strings will be more probable than others, with the set of probabilities comprising the output of the benchmark that have to be compared against the correct values. We use this method because we know that if you choose the gates at random, it is a hard computational problem for classical computers, but not as hard for quantum computers.
Cross-entropy benchmarking and a quantum supremacy experiments use two different meanings of the word “benchmarking.” One is trying to measure the worst-case equivalent computational power of the quantum computer. The second is to assess the fidelity or accuracy of the experimental quantum computer, which is important to help design the next generation system as well as to learn the “control map” that adjusts control signals on the fly to compensate for manufacturing variance.
So what is the cross-entropy metric? We compute the probability of some data stream Q by sampling the output of the experimental quantum computer millions of times. There are other observables, such as the heavy output score introduced by Aaronson and Chen, and we use a new chip the hardware group has developed called Sycamore with 54 Xmon qubits, Xmons are a version of transmons. The new feature in Sycamore is that the couplers between the qubits are adjustable, which is how we create random gates without remanufacturing the chip.
Google’s road map is to create a fault tolerant computer, which will require error rates about 10 times lower than the error correction threshold, which is around 10-2 error rate, so we will need 10-3. After this, we will scale the number of qubits.
We already perform cross-entropy benchmarking the whole system, not just simultaneous two-qubit gates. We fix the circuit’s depth to 14 cycles of two-qubit gates with single qubit gates in between, which means the quantum circuit is really 28 clock cycles. An equivalent supercomputer simulation takes 5 hours for one circuit and there were 10 simulations running in parallel on a million cores, so this is 50,000,000 core hours—which we ran on Google clusters.
In terms of classical simulation algorithms for the run time comparison, there is the Schrödinger algorithm, which stores the entire quantum state in RAM. Nobody has implemented such an algorithm that goes beyond that references 48 qubits, but IBM is exploring the use disk.
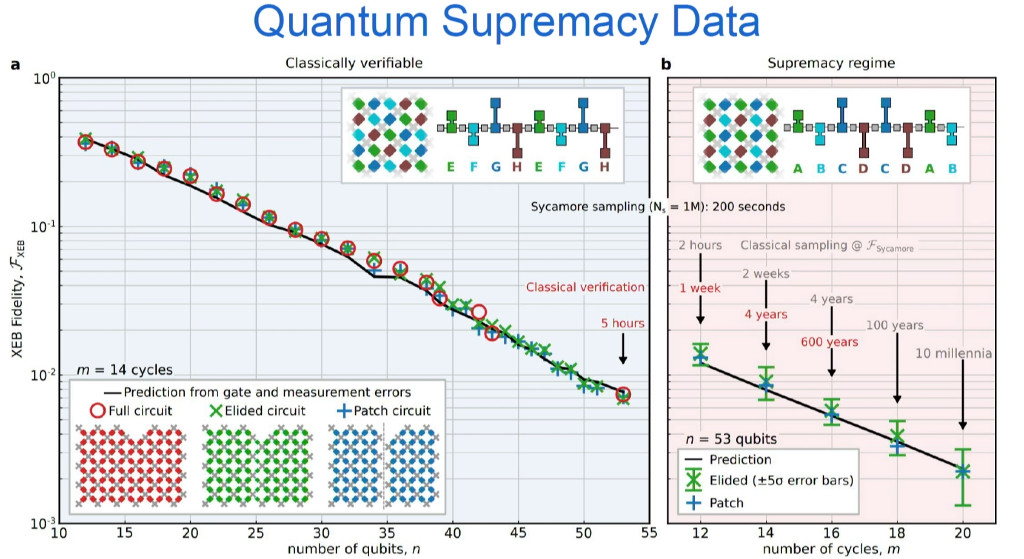
We expect quantum hardware will also keep improving, so the race is on for both more capable quantum chip and larger classical simulations. So, it will be very important for IBM to run its improved classical simulation algorithms, which will face challenges due to scale such as failures, checkpointing to recover from failures, high energy consumption, and other nightmares that arise for any large supercomputer run.
See video by Sergio Boxio, Cross Entropy Benchmarking and Quantum Supremacy, duration 34:45
What is quantum algorithmic breakeven for quantum annealers?
Rather than focusing on single- and two-qubit errors, the larger scale of quantum annealers is sufficient to actually look ahead and talk about speedup. This leads to a new concept called quantum algorithmic breakeven.
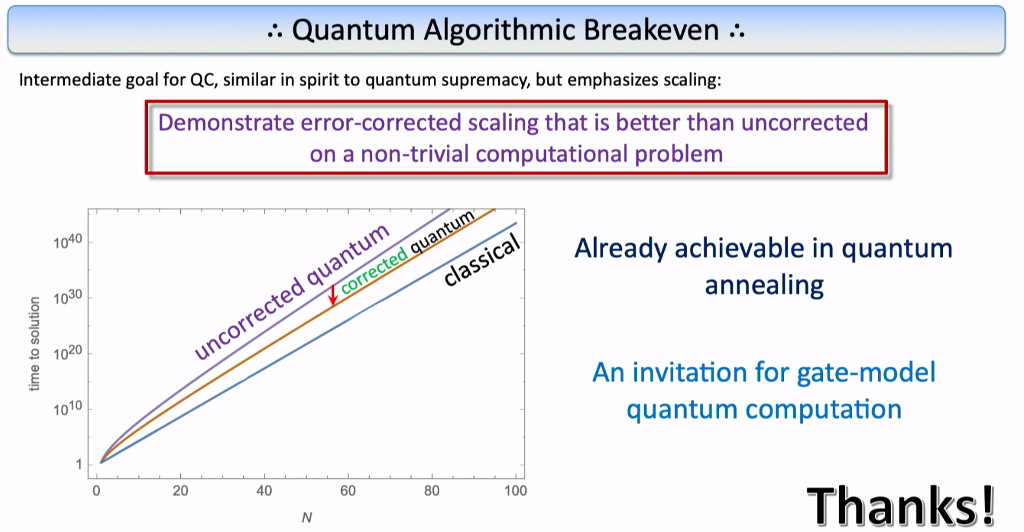
To understand quantum speedup, let’s first clarify that it is not an about actual runtime. Actual runtime is highly dependent on which classical supercomputer you measure your quantum system against. Instead, quantum speedup is about scaling with respect to the time to solution. A quantum speedup could be exponential scaling for a classical algorithm versus a polynomial scaling for a quantum algorithm--or a lower exponent when we're experiencing exponential scaling in both cases—or maybe a lower degree polynomial if we're talking about polynomial scaling and the quantum exponent is less than the classical exponent.
The recent spat between Google and IBM it's an example of an argument about IBM’s claim of 2½ days classical simulation time versus Google’s claim of 10,000 years. However, this is an argument about actual run time, which according to the definition discussed here is not really related to quantum speedup.
Imagine the following dream scenario. The quantum computer’s time to solution on a semi log scale would be polynomial for some algorithm, such as quantum simulation, in the ideal case where there's no decoherence and no control errors. However, the classical time to solution would be exponential. We would see a beautiful separation on the graph where the quantum scaling advantage is clear for every problem size. But unfortunately, this has not been observed on any quantum hardware to date.
A more realistic scenario is we have some decoherence and then the quantum polynomial scaling is somewhat worse. The exponent could be higher, so perhaps we would not see a speedup when the number of qubits is small and the quantum scaling advantage only becomes clear for larger N. It's reasonable to assume current NISQ-era quantum systems follow this scenario.
Now let’s look at algorithmic speedup. The only current quantum systems of sufficient scale to assess algorithmic speedup quantum annealers. So for a particular work we published last year,2 we actually demonstrated a speedup of time to solution on a D-wave, or showing time to solution as a function of problem size for scaling better for D-Wave was better than classical simulated annealing. Now why was this not published in Nature and made it to the New York Times?
Because the classical algorithm was not the best one. And Unfortunately for D-Wave, when we compared its performance against other algorithms, it lost.
However, there's something you can do for annealers that is similar to randomized techniques, called dynamical coupling, it is a very primitive type of error suppression method.
So let's go back to the shape of the graph discussed above and see if there is hope for quantum error correction on annealers? The goals would simply be to demonstrate that quantum error correction can take uncorrected quantum scaling, push it down a little bit, so that perhaps it is still not better than a classical computer, but you are demonstrating that error correction helps in terms of the time to solution metric relative to the uncorrected setting. So, what is algorithm breakeven with quantum error correction? It’s the idea of demonstrating a corrected quantum scaling that is better than the uncorrected quantum scaling, but it doesn't necessarily have to be better than classical—that bar is too high for NISQ-era devices.
We observed the time for solution as a function of problem size increasing on a semi-log scale roughly exponentially without error correction. The clincher is that scaling improved with error correction.
We reached this point 5 years ago but have made progress on a more challenging goal since then. Five years ago we only had 500 qubits and didn't look at that control errors, so now we have 2,048 qubits and can now account for control errors.
After many millions of experiments without error correction, the number of runs or the time to solution required to find a certain ground state, plotted on a semi log scale as function of the number of qubits, with added noise, showed that as you add more noise the scaling increases dramatically, i.e. super exponential. What happens with error correction, with the quantum annealing correction method described above, is what happens to the scaling. So once again this is an example of algorithmic breakeven in the sense that the uncorrected versus the corrected scaling is better you can eyeball it for every value of noise and for every value of qubits it's true that that the result is better for the corrected setting.
So, we have introduced a notion of quantum algorithmic breakeven, which is the idea that we should demonstrate an error corrected scaling that is better than the uncorrected scaling on a non-trivial computational problem. It’s early days for NISQ processors but its moving in the direction where these kind of demonstrations should become possible.
See Quantum Algorithmic Breakeven: on scaling up noisy qubits, Daniel Lidar. 55:13 to 1:34:05
How is Quantum Computer Performance Measured?
This talk covers volumetric randomized benchmarking and mirror networks. This work on scalable benchmarking originated in the Quantum Performance lab at Sandia National Laboratories. The talk first discusses why we need to do benchmarking quantum computers in the first place. Volumetric benchmarking is the framework of the solution discussed, but you also need circuits to actually run in the framework, for which Sandia developed mirror circuits. The talk also shows experimental results.
What are we trying to benchmark? Unlike standard classical computers, the components in a quantum computer fail frequently, forming the main limiting factor with quantum computers.
What are some examples of quantum computer errors?
- Bit flips, just like in classical computers
- Failure modes unique to quantum computers, such as errors that add up coherently
- Drift in performance over time, based on the fact that quantum computers are analog
- Cross talk
- Integration failures where a device doesn't actually perform as well as the sum of its parts
Real quantum computer errors have to be explained in the context of real devices, and we’ll use the publicly available IBM Q Tenerife from IBM quantum experience as an example. The device’s website shows the name of the device and graph showing its 5 qubits in a particular layout and a spec. For example, the gate error rate for qubit 0 is 0.1% for gates on just that qubit and a 2-qubit gate between qubit 0 and qubit 1 has an error rate of 0.3%. Multiply those numbers together and subtract from 1 using basic and probability theory and you get 15%. So, for this particular circuit you would think that the chance of failure is 15%.
The reality is that this doesn't work generally because it ignores almost all structure in the circuit, or where different errors interact with different structures in complicated ways, such as emergent noise, crosstalk, and so on.
So we need more than low-level benchmarks. This talk presents some approaches, but other recent developments include cycle benchmarking presented elsewhere at this workshop.
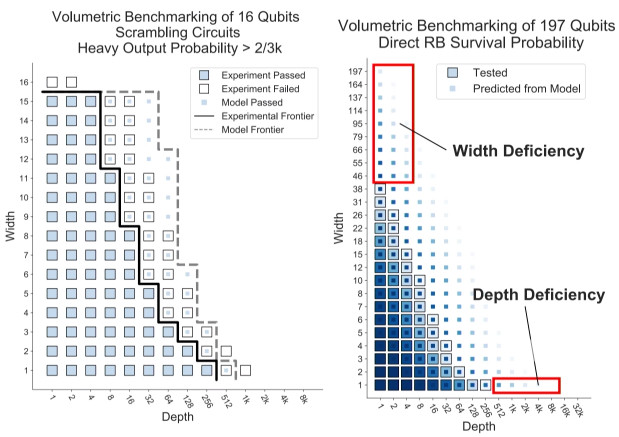
Sandia developed a volume metric benchmarking framework, inspired by IBM's work on quantum volume. IBM recognized that adding more qubits doesn't increase computational power if there's going to be an error before all the qubits can interact with each other. You essentially have a smaller device than your thought you had. Furthermore, decreasing error rate won't actually increase computational power if you can already access all the states. So, IBM defined the effective size of the device as the largest number of qubits for which you can access the entire state. In more detail, the quantum circuits have both width and depth equal to D and they’re a type of scrambling circuit. The quantum volume is defined as 2D*, where D* is the largest D for which the circuit computes the correct answer with acceptable reliability.
Quantum volume is a pretty nice way to benchmark a quantum computer, but it does not give a complete measure device performance. Unfortunately, real programs process data in accordance with an algorithm, which often has different properties than a D×D random scrambling network. For example, the straightforward implementation of Shor’s algorithm has order n qubits and order n3 depth, yet other algorithms that have lower depth than the number of qubits. Another complication is that we don't know yet what algorithms will be important for quantum computers.
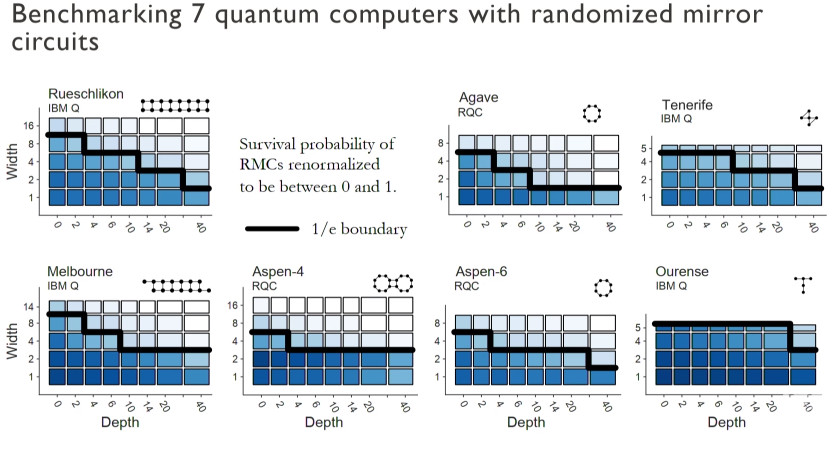
So. this inspires the volumetric benchmarking framework we've been developing. Sandia defines a volumetric benchmark as a map from widths and depths to a measure of success for an ensemble of circuits at each width and depth. The plot below shows exemplary data just to demonstrate how the method allows a person to visualize the data from these methods. Each data point shows weather the circuit succeeded or failed with a binary success or failure measure. The blue squares are where circuits were successful and white where it failed. The frontier is where we can no longer run the circuit successfully. We can compare the predictions of this spec sheet, for example from IBM, Rigetti, or some new device you’re evaluating.
What are Mirror Circuits?
Sandia developed a specific class of circuits called mirror circuits to facilitate volumetric benchmarking. Their general structure is based on motion reversal and consists of:
- A general D-input unitary in 2 layers, i.e. a quantum gate network
- A layer of local randomization on each qubit
- The inverse of the previous unitary in D over 2 more layers
Within this framework there may different things you could do:
- The unitary could be a random circuit, and then you run the random circuit in reverse, undoing the calculation and giving the original input back. The output should be the same as the input, making it easy to check correctness.
- The unitary could be based on a structured circuit, such as one layer or perhaps a few layers in repetition to see how structure impacts performance
We have principally considered circuits that only contain only Clifford gates and so that and the randomization is a Pauli, which means that the outcome is a fixed bit stream that a classical computer can easily calculate.
We benchmarked 12 different quantum computers, with results from 7 shown below, including devices from IBM and Rigetti Computing. For Agave, for example, the black line that shows the threshold beyond which we can no longer run these circuits. So, for example, we can run out to depth six for two qubits but we can't go out to depth ten.
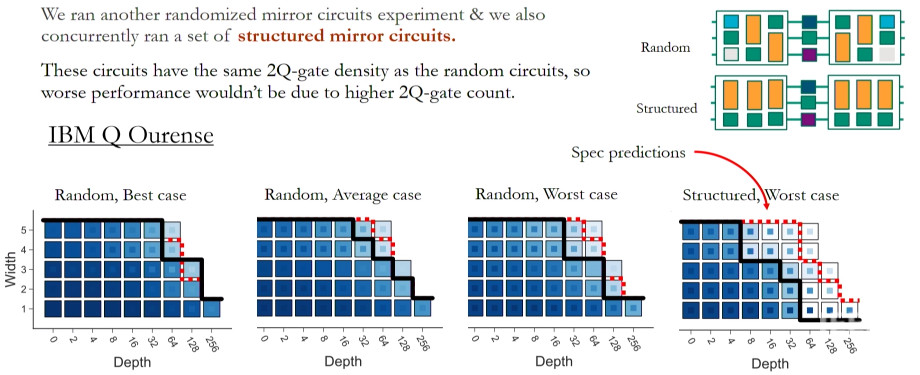
Structured Circuits
Structured circuits could be very different in general, so let’s combine ideas and consider a set of structured mirror circuits. The plot below shows what we get when we run on IBM Q Ourense with their recent devices, showing random best average and worst case again just like before and then there's structured worst case and what you can see is that the structured performance is much worse than the other cases, so the structure is really causing a big impact and this is a clear sign of coherent errors.
See the video for more information. Essentially, holistic benchmarking is clearly important as many sources of error only emerge at scale, making current types of performance data insufficient to predict performance. We developed a general framework around volumetric benchmarking and some specific classes of circuits for the framework including randomized and structured mirror circuits. The circuits scale and we've run them on all the quantum computers that are currently publicly available. The results show the predictive power of spec sheets varies a lot between devices but they're generally not very predictive and they’re overoptimistic of how good devices how well devices actually perform. Our work also shows that circuit structure matters, so just giving a set of gate error rates is not enough. In addition, performance on standard randomized benchmarks doesn't guarantee good performance on real application circuits. It's going to be very important to carefully benchmark computers in the near term and we think mirror circuits are good candidate for this.
See Demonstrating Scalable Benchmarking of Quantum Computers, Tim Proctor.
References
[1] Arute, Frank, et al. "Quantum supremacy using a programmable superconducting processor." Nature 574.7779 (2019): 505-510.
[2] Albash, Tameem, and Daniel A. Lidar. "Demonstration of a scaling advantage for a quantum annealer over simulated annealing." Physical Review X 8.3 (2018): 031016.
Education
- Details
- Written by John Wettlaufer
- Category: Education
 This online community is intended to help educate and inspire the next generation of QIS scientists and engineers.
This online community is intended to help educate and inspire the next generation of QIS scientists and engineers.
Quantum Information Science (QIS) is at a historically important juncture.
- Its laboratory bona fides have been firmly established; now, scientists and engineers at scores of companies and institutes are racing to transform lab projects into scalable, production-ready systems that can be turned loose on real-world problems.
The situation gives rise to a number of questions.
- What expectations should society, especially those involved in setting government policy, have for the near- and longer-term future of quantum machines?
- What should today's science and engineering students be taught about the growing body of quantum information sciences?
- Might a shortage of skilled workers hamper the roll-out of robust quantum systems?
There is rapid funding now available in quantum computing, like the billion-dollar National Quantum Initiative and likely industry co-investment.
- The immediate problem is that there are not enough workers trained in quantum information to effectively spend the projected funds. These immediate needs could be addressed by incremental education, such as one or two courses that would allow a skilled circuit designer, for example, to design quantum circuits -- or a materials researcher to be able to study quantum information behaviors in qubits
Quantum Education Portal
The Quantum Education Portal is the home of the educational activies of the IEEE Quantum Education Interest Group.
Within the IEEE Quantum Initiative, the Quantum Education Interest Group creates and currates educational materials suited for educational level ranges from STEM to post graduate and degree programs through night school.
Visit the Quantum Education Portal
Articles
 What is Quantum Engtanglement? Skip the heady and abstract physics lectures. Let’s talk about socks
What is Quantum Engtanglement? Skip the heady and abstract physics lectures. Let’s talk about socks
08 June 2022 | IEEE Spectrum
When pushed to explain why quantum computers can outspeed classical computers, stories about quantum computing often invoke a mysterious property called “entanglement.” Qubits, the reader is assured, can somehow be quantum mechanically entangled such that they depend on one another.
Summary of the 2019 IEEE Workshop on Benchmarking Quantum Computational Devices and Systems
 7 November 2019 | San Mateo, California, USA
7 November 2019 | San Mateo, California, USA
A summary and speaker presentations on the topics of quantum supremacy and quantum computer performance are now available from our half-day workshop on benchmarking quantum computational devices and systems. The workshop was held in conjunction with the 2019 IEEE International Conference on Rebooting Computing (ICRC) and was part of IEEE Rebooting Computing Week 2019.
Resources
Satellite-Based Continuous-Variable Quantum Communications: State-of-the-Art and a Predictive Outlook (Open Access)
IEEE Communications Surveys & Tutorials, Volume 21, Issue 1
IEEE GLOBECOM 2016 Tutorial: Quantum Communications (PDF, 6 MB)
Rob Malaney, UNSW
Videos
Introduction to Quantum
University Lectures
Innovations in Industry

































